强化学习用于解决怎样的问题 | 基本的强化学习算法 | CS188 Project 3

Motivation

在P4中，我们讨论了如何利用Value Iteration等算法解决MDP问题，这些算法的基本特征是其事先拥有计算optimal policy所需的全部信息。（参考如下贝尔曼方程，所需的全部信息无非$T,R$）
$$
V^{\star}(s)=\underset{a}{max}\underset{s’}{\sum}\space T(s,a,s’)[R(s,a,s’)+\gamma V^{\star}(s’)]
$$
如果$T,R$未知，我们就需要依靠Learning来获取需要的信息。Learning有很多种，最基础的是监督学习和强化学习。

  • 监督学习：事先有一些标注好的数据，学习的过程就是训练Agent在遇到类似情况时按照标注数据行动。

    监督学习有两大难点：一是标注数据很难覆盖全部情况，比如在棋类游戏中，很难有一个大师数据库能提供所有状态下正确的走法；二是很多应用场景没有标注数据。在这种场景中就需要用到强化学习

  • 强化学习：Agent不断与环境交互并获得反馈，利用这些反馈来修正自己的行为。反馈其实也属于先验知识，但它往往比较清晰简单，比如下棋时的胜负，赛车时是否沿赛道行进等。这是强化学习与监督学习本质不同的地方，强化学习所需要的先验知识很简单就能获得，无需标注数据。

根据要学习的目标不同，强化学习可分为两种，以MDP为例：

  1. Model-based Learning: 通过Learning获得$T,R$，然后再求optimal policy
  2. Model-free Learning: 直接学习values/q-values

根据Agent的行为是否改变，强化学习又可分为两种：

  1. passive: 事先给定一个policy $\pi$, Agent完全按照$\pi$与环境交互并收集反馈完成学习。
    • 如果是model-free, 那学习的目标就是$V^{\pi}(s)$, 否则将是Transition model.
    • 因为固定$\pi$显然没办法获取MDP的全部信息，因此passive reinforcement必须和其它方法结合起来使用才能求出真正的optimal policy
  2. active: Agent一边学习一边修正自己的行为，直到学出optimal policy.
    • Agent必须尽可能多地与环境产生不同交互才能习得全部知识，这个阶段称为exploration. 与此同时，Agent也需要将自己的行为逐渐收敛到optimal policy，这个阶段称为exploitation. 如何平衡分配在两个阶段花费的时间是一个值得讨论的话题。

Model-based Learning

Model-based Learning算法直接估计$T,R$的估计值$\hat{T},\hat{R}$.

计算$\hat{T}$

选定一个随机的policy $\pi_{explore}$记录从$(s,a)$到$s’$的次数$Cnt[(s,a,s’)]$, 以及到达q-state$(s,a)$的总次数$Cnt[(s,a)]$. 则有：

$\hat{T}(s,a,s’)=Cnt[(s,a,s’)]/Cnt[(s,a)]=f(s’|a,s)$. 其中$f$表示事件的频率

事实上，MDP具有如下性质：$T(s,a,s’)=P(s’|a,s)$. 根据大数定律，当取样次数足够多时，$\hat{T}$将收敛到$T$

之后尝试不同的policy求出所有$T$

计算$\hat{R}$

从q-state$(s,a)$转移到$s’$时，$R(s,a,s’)$就获知了。因此只要尝试不同的policy直到所有$R$已知即可。

在求出$T,R$后，应用P4中讨论过的Policy Iteration即可。

这种方法的弊端是我们需要维护每个tuple的$Cnt$，memory overhead很大。

Model-free Learning

  1. passive reinforcement learning
    • 给定policy $\pi$, 学习出$V^{\pi}(s)$.
  2. active reinforcement learning

Direct Evaluation

DE是一种passive reinforcement learning：确定一个随机的policy $\pi$,然后不断采样，统计每个状态$s$获得的总收益$totalValue$, 以及所有样本中到达状态$s$的次数$Cnt$. 采样足够多次数后，$V^{\pi}(s)=totalValue(s)/Cnt(s)$.

这个想法相当直观，因为$\pi$已经确定，那么从状态$s$出发到终止状态$s_t$所经过的每种状态迁移序列的出现概率 × 该序列收益即为$V^{\pi}(s)$.

采样次数足够多时，$totalValue(s)$中各个tuple$(s,a,s’)$出现的频率收敛到概率，因此等式成立。

这种方法的弊端是需要采样足够多次数，否则结果与真实值相差较大。

Temporal Difference Learning

TD-Learning也是一种passive reinforcement learning，它的核心思想是从所有经验中学习。要理解这个思想，首先回顾DE的做法————对于每个样本$(s,a,s’)$，DE仅仅记录其产生的收益和次数，并没有完全利用这里面的状态转移信息。

我们将passive reinforcement learning的目标重新表述为：在不求$T$的情况下直接解下列方程组，更一般的来说就是在不知道权重的情况下求加权平均。TD-Learning通过指数移动平均法达成上述目标。
$$
V^{\pi}(s)=\sum_{s’}T(s,\pi(s),s’)[R(s,\pi(s),s’)+\gamma V^{\pi}(s’)]
$$

  • 初始化$V^{\pi}(s)=0$

  • 对于每一次状态转移$(s,\pi(s),s’)$, 可以得到值$sample=R(s,\pi(s),s’)+\gamma V^{\pi}(s’)$. 该值实际上是对$V^{\pi}(s)$的新估计值。接下来就要把新估计值以某种方式加入到之前的估计值中（反馈）。具体地，我们采用如下更新策略：
    $$
    V^{\pi}(s)\leftarrow(1-\alpha)V^{\pi}(s)+\alpha* sample
    $$
    其中, $0\leq \alpha \leq 1$. 其含义为学习速率，表示我们对新估计值的认可程度。很显然，当$V^{\pi}$贴近真实值时, $\alpha$越小，收敛速率越快反之亦然。一般来说，整个学习过程中$V^{\pi}$是越来越贴近真值的。因此通常在一开始指定$\alpha=1$, 然后逐渐减小$\alpha$的值。

    从另一个方面我们也能看出这个更新公式有效的原因，即使假设$\alpha$不变，展开递推式易得:
    $$
    V^{\pi}k(s)=\alpha\cdot[(1-\alpha)^{k-1}\cdot sample_1+…+(1-\alpha)\cdot sample{k-1}+sample_k]
    $$
    因为$0\leq1-\alpha\leq 1$, 因此越老旧的样本在后期比重越小。这很符合直观，因为随着算法的不断迭代，样本的准确值是逐渐上升的，我们当然希望准确的样本能占比更多。

  • 不断迭代直到收敛

再次理解从所有经验中学习：在TD-L中，每一个样本包含了状态转移的信息且都在最终的结果有一席之地。

Q-Learning

DE和TD-L从本质上来说都只是在求$V^{\pi}$, 而要想真正得到optimal policy还需要借助其它手段，比如model-based learning等。而求出$Q^{*}$则可直接导出optimal policy.

首先，如果$T,R$已知，我们可通过q-value iteration求解，其迭代式如下：
$$
Q_{k+1}(s,a)=\sum_{s’}T(s,a,s’)[R(s,a,s’)+\gamma \space \underset{a’}{max}Q_k(s’,a’)]
$$
然而，权重未知。但这和TD-L形式完全一致：在不知权重的情况下求加权平均。因此继续采用指数移动平均法即可求解。
$$
sample=R(s,a,s’)+\gamma \space \underset{a’}{max}Q_k(s’,a’)
$$

$$
Q(s,a)\leftarrow (1-\alpha)Q(s,a)+\alpha*sample
$$

Approximate Q-Learning

Q-L已经足够好了，美中不足的是为了执行该算法需要维护所有的q-value. 一旦状态数太多(而这十分常见)，很容易就会超过计算机内存限制。而很多状态其实是“相似”的，没必要逐个学习其q-value而是可以举一反三。

图1

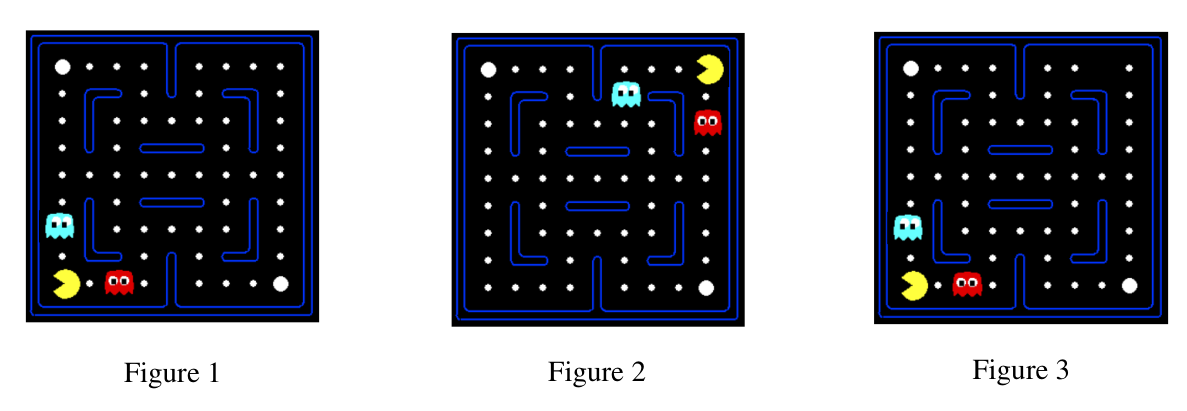
以上图为例，Figure1,2,3分别代表三种q-state。在传统Q-L中需要分别维护其q-value然后逐渐迭代收敛。但实际上只要习得Figure1对应的q-value，发现这种状态收益差，就可以直接推断出Figure2、Figure3收益也差，而无需再逐次收敛求解。

这种idea本质上就是只学习具有代表性的情况。换句话说，我们需要将原来state的本质特征抽象表示为特征向量，进而可得出:
$$
V(s)=w_1\cdot f_1(s)+w_2\cdot f_2(s)+…+w_n\cdot f_n(s)=\vec{w}\cdot\vec{f}(s)
$$

$$
Q(s,a)=\vec{w}\cdot \vec{f}(s,a)
$$

其中$f_i$表示特征函数，比如在Pacman中可以是距离最近gohst的距离

对$V(s)$的重构使得我们的问题变成了学习参数$\vec{w}$，操作如下：

定义$diff=[R(s,a,s’)+\gamma \space \underset{a’}{max}Q_k(s’,a’)]-Q(s,a)$, 则更新规则如下:
$$
w_i\leftarrow w_i+\alpha\cdot diff\cdot f_i(s,a)
$$
如此，我们就只需要在内存中维护$\vec{w}$, 在学习结束后按需计算$Q^{*}$即可。

Q: AQ-L的idea和最终的算法是怎么联系到一起的？

在上文中我们看到AQ-L的启发式动机是，在Q-L中学习了大量重复的内容。因此为了优化，我们希望的是对于相似的情况只学习一遍，其它情况由这一遍习得的结果推断得出。这个idea促使我们不再学习具体的state’s value，而是学习从相似states中抽象而来的特征的value. 而一旦抽象出特征，value就可立马表示成线性值函数，需要学习的内容进一步变成了值函数的参数。

Exploration and Exploitation

$\epsilon$-Greedy

想法非常简单，选定$\epsilon\in[0,1]$。

在每一次选择action时以概率$\epsilon$采用random policy（即在所有legalActions中随机选择）, 以概率$1-\epsilon$采用当前的estimated optimal action.

在实际应用中$\epsilon$需要人为tune. Project3中有类似的题目，见下文。

Exploration Functions

更新规则变为:
$$
Q(s,a)\leftarrow (1-\alpha)Q(s,a)+\alpha\cdot [R(s,a,s’)+\gamma \underset{a’}{max}f(s’,a’)]
$$
$f$有很多种定义，较为常见的是如下:
$$
f(s,a)=Q(s,a)+\frac{k}{N(s,a)}
$$
其中$k$是一个提前确定的常数,$N(s,a)$表示该q-state被访问的次数

Q: Exploitation和Exploration分别有什么意义？

指数平均移动法收敛到一个q-value的真值需要多轮采样。学习完毕后Agent的行为是利用学到的q-values计算optimal policy，因此学习阶段的目标是让真正optimal的q-state“凸显”出来。如果没有exploitation阶段，那最优策略的收益离真值较远，有可能被次优解给挤掉了。形象一点来说，exploitation阶段的目标是发掘当前最优策略的真正价值，避免被埋没。

当然，也不能只有exploitation，这同样会使得最优解不一定被发现。

CS188 Project3

Q1 Value Iteration

将贝尔曼方程原模原样搬上来即可。稍微值得注意的是，每一轮迭代更新$s$时依赖的$state$可能已经被更新了，因此需要先保存所有$states$上一轮迭代的值用作更新。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
def runValueIteration(self):
    for i in range(0, self.iterations):
        incrementVector = util.Counter()
        for s in self.mdp.getStates():
            maxValue = -9999
            actions = self.mdp.getPossibleActions(s)
            if len(actions) == 0:
                maxValue = 0
        	for a in actions:
                    sum = 0
                    for sp_tuple in self.mdp.getTransitionStatesAndProbs(s, a):
                        succ, prob = sp_tuple
                        reward = self.mdp.getReward(s, a, succ)
                        sum += prob * (reward + self.discount * self.values[succ])
                    maxValue = max(sum, maxValue)
                incrementVector[s] = maxValue - self.values[s]
            self.values = self.values + incrementVector
            
def computeQValueFromValues(self, state, action):
    sum = 0
    for sp_tuple in self.mdp.getTransitionStatesAndProbs(state, action):
        succ, prob = sp_tuple
        reward = self.mdp.getReward(state, action, succ)
        sum += prob * (reward + self.discount * self.values[succ])
        return sum

def computeActionFromValues(self, state):
    cnt = util.Counter()
    actions = self.mdp.getPossibleActions(state)
    if len(actions) == 0:
        return None
    for action in actions:
        for sp_tuple in self.mdp.getTransitionStatesAndProbs(state, action):
            succ, prob = sp_tuple
            reward = self.mdp.getReward(state, action, succ)
            cnt[action] += prob * (reward + self.discount * self.values[succ])
    return cnt.argMax()

Q2 Bridge Crossing Analysis

这题很有意思，让你自己调整MDP的参数使得Agent的行为符合预期规定。通过这题可以很好地体验各个参数的作用。
$$
discount=0.9,noise=0
$$

Q3 Policies

Q3和上题考察目标一样，不过地图变得更加复杂了。

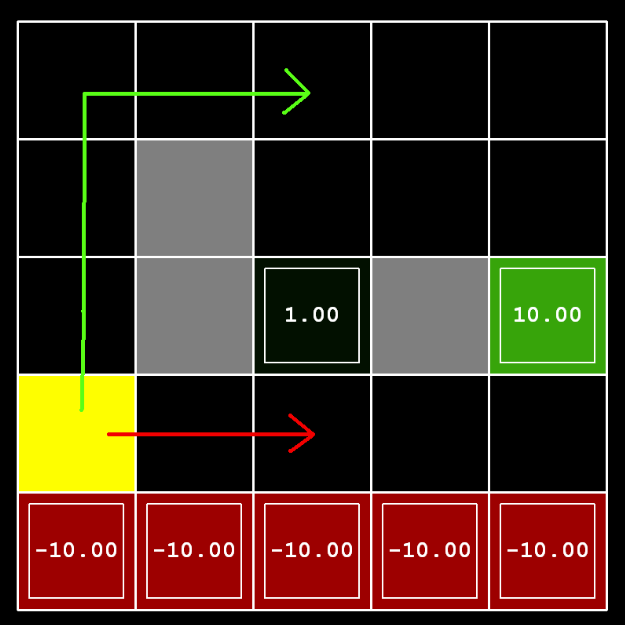
image-20220908170521798
目标 discount noise living reward 解释
冒险去+1 0.01 0 0.01 尽快结束(高衰变率)，不易落入陷阱(低随机性)
避险去+1 0.2 0.2 0.01 尽快结束，易落入陷阱
冒险去+10 0.9 0 0.01 不用尽快结束，不易落入陷阱
避免去+10 0.9 0.5 0.01 同理
既不想结束也不想落入陷阱 0.1 0.2 0.01 活着的收益比结束带来的收益大，略微减少discount即可

Q4 Asynchronous Value Iteration

和Q1基本相同，唯一区别在于这回一次迭代只更新一个$state$, 因此依赖的其它$state$都是最新值。

1
2
3
4
5
def runValueIteration(self):
    states = self.mdp.getStates()
    for i in range(0, self.iterations):
        state = states[i % len(states)]
        self.values[state] = computeMaxQvalue(state, self.mdp, self.discount,self.values)

Q5 Prioritized Sweeping Value Iteration

用优先级队列优化迭代。

ValueIteration的目标是尽可能早地迭代至不动点，此时就一定是最优解。引入优先级队列就是要让最有可能造成policy改变的state优先迭代。

  • 怎样的state最可能改变自己当前的optimal action？

    $$ V(s)=\underset{a}{max}[Q(s,a)] $$

    根据上述公式，即问最大$Q(s,a)$中的a什么时候最可能发生改变？

    答案是：如果在迭代后继节点时造成$maxQ$与当前的$V$差值较大，此时更可能改变。但并不是一定，因为有可能是相同action对应的Q发生大改。但这种启发式的衡量方式计算简便且准确度并不低。

  • 为什么要引入临界值$\theta$？

    当差值较小时，我们不希望重新把前驱结点加入更新队列，$\theta$用于衡量这一临界值。换句话说，$\theta$越大，迭代次数就越少，迭代结果就越不准确。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
def runValueIteration(self):
    states = self.mdp.getStates()
    #compute all predecessors.
    predecessors = {}
    for state in states:
        successors = set()
        for action in self.mdp.getPossibleActions(state):
            for succ in self.mdp.getTransitionStatesAndProbs(state, action)[0]:
                successors.add(succ)
        for succ in successors:
            if not succ in predecessors:
                predecessors[succ] = set()
            predecessors[succ].add(state)

    #initialize priority queue.
    priority_queue = util.PriorityQueue()
    for state in states:
        diff = abs(computeMaxQvalue(state, self.mdp, self.discount, self.values) - self.values[state])
        priority_queue.push(state, -diff)

    #iteration
    for i in range(0, self.iterations):
        if priority_queue.isEmpty():
            break
        state = priority_queue.pop()
        self.values[state] = computeMaxQvalue(state, self.mdp, self.discount, self.values)
        for pred in predecessors[state]:
            diff = abs(computeMaxQvalue(pred, self.mdp, self.discount, self.values) - self.values[pred])
            if diff > self.theta:
                priority_queue.update(pred, -diff)

Q6 Q-Learning

当你理解了Q-Learning为什么work后，这一节无非就是把公式转换为代码罢了。

1
2
3
def update(self, state, action, nextState, reward):
    sample = reward + self.discount * self.computeValueFromQValues(nextState)
    self.qvalues[(state, action)] = self.getQValue(state, action) * (1 - self.alpha) + sample * self.alpha

Q7 Epsilon Greedy

1
2
3
4
5
6
def getAction(self, state):
    if util.flipCoin(self.epsilon):
      action = random.choice(legalActions)
    else:
      action = self.computeActionFromQValues(state)
    return action

Q8，Q9都不用修改代码，只要前面的代码足够general即可

Q10 Approximate Q-Learning

同上，只要理解了公式，代码无非就是表达公式。

1
2
3
4
5
6
7
8
9
10
11
12
def getQValue(self, state, action):
    qvalue = 0
    features = self.featExtractor.getFeatures(state, action)
    for feat in list(features.keys()):
      qvalue += self.weights[feat] * features[feat]
    return qvalue

def update(self, state, action, nextState, reward):
    diff = reward + self.discount * self.computeValueFromQValues(nextState) - self.getQValue(state, action)
    features = self.featExtractor.getFeatures(state, action)
    for feat in list(features.keys()):
      self.weights[feat] += self.alpha * diff * features[feat]

这道题在正确性之外有一点值得注意：

经典Q-Learning在Pacman地图size很小时表现尚可，可一旦地图扩大，学2000轮都还是在乱走；而使用近似Q-Learning后，学50轮就表现得非常不错了，为什么？

  • 地图size扩大后，状态数激增（经典Q-Learning中地图上任意一点不一样都是不同state），因此学习阶段能覆盖的policy占比很少。换句话说，即使学习时间全部用于exploration，都可能还没覆盖到optimal policy。
  • 近似Q-Learning抽取原来状态的重要特征，泛化了学习。因此能够在尽可能少的学习时间里，找到最优解。

这个现象说明近似Q-Learning不光节省空间，只要特征抽取合理也能极大地提高学习效率。