CS188-P4 Markov decision process
在P1和P3中我们分别讨论了传统的搜索问题以及确定性零和博弈问题,它们都有一个共同的特征: 在状态$s$采取行为$a$,发生的状态转移是确定的。然而,实际生活中有非常多的问题充满不确定性(像扑克、麻将等),因此我们需要对这种不确定性进行建模————马尔科夫决策过程(MDP)。
Dynamic Programming
不同于算法课中的动态规划算法,这里的DP指的是一种数学优化方法。
Dynamic decision problem
DP要解决的问题统称为dynamic decision problem, 它们具有如下形式:
- 在$t$时刻的状态称为$x_t$。特别地,初始状态记为$x_0$
- 在任意时刻可采取的行动取决于当前的状态,记为$a_t\in\Gamma(x_t)$
- 在状态$x$采取行动$a$将转移到的状态由$T(x,a)$确定,收益由$F(x,a)$确定. (先不考虑随机性)
- 引入discount factor $\gamma$表示收益随着时间指数级递减
- $V(x)$表示从状态$x$出发能获得的最大收益
则有:
$$
V(x_0)=max_{a_t}\Sigma_{t=0}^{\infin}\gamma ^t F(x_t,a_t)
$$
直观来讲就是遍历所有可能采取的行动的组合,最大值则为初始状态能获得的最大收益。
Bellman Equation
上式显然是难以直接计算的。但根据定义,我们可以得出如下结论:
Principle of Optimality: 一个最优策略具有这样的性质————无论初始状态$x_0$和初始决策$a_)$是什么,之后的决策对于$T(x_0,a_0)$都构成最优策略。
这个结论其实就是DP算法中的最优子结构。有了这样一个结论,上式就可改写为递推式:
$$
V(x_0)=\underset{a_0}{max}{F(x_0,a_0)+\gamma V(T(x_0,a_0))}
$$
这就是贝尔曼方程。此时,求解(1)式就变成了求解(2)中的函数方程。
如果引入了不确定性,即之前的$T(x,a)$有多个解,我们只需要转而求数学期望即可。
Marcov decision process
- $S$是所有states的集合
- $A$是所有actions的集合
- start state
- one or more terminal states
- discount factor $\gamma$
- 转移函数$T(s,a,s’)$, 值为在状态$s$采取action $a$,状态转移到$s’$的概率
- 回报函数$R(s,a,s’)$, 值为在状态$s$采取action $a$,状态转移到$s’$的回报。通常来说每一步都有一个小回报,转移到terminal state则是大回报,用于刻画实际决策过程。
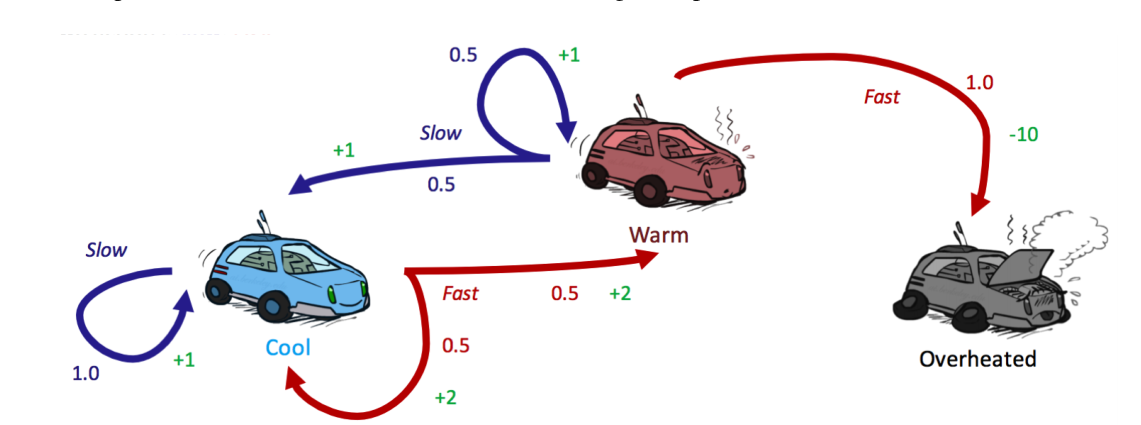
上图是一个具体的例子,汽车有三种状态,在每种状态下采取行动会以不同概率转移到其它状态。
通常,对于一个MDP问题,我们希望求解的是在到达terminal state之前,如何决策才能使回报最大。有时,我们还希望限制决策的时间,即要在有限时间内回报最大。以上图为例,如果不限时间,永远在Cool状态选择slow action,将永远不会到达terminal state,回报也一直在上升。
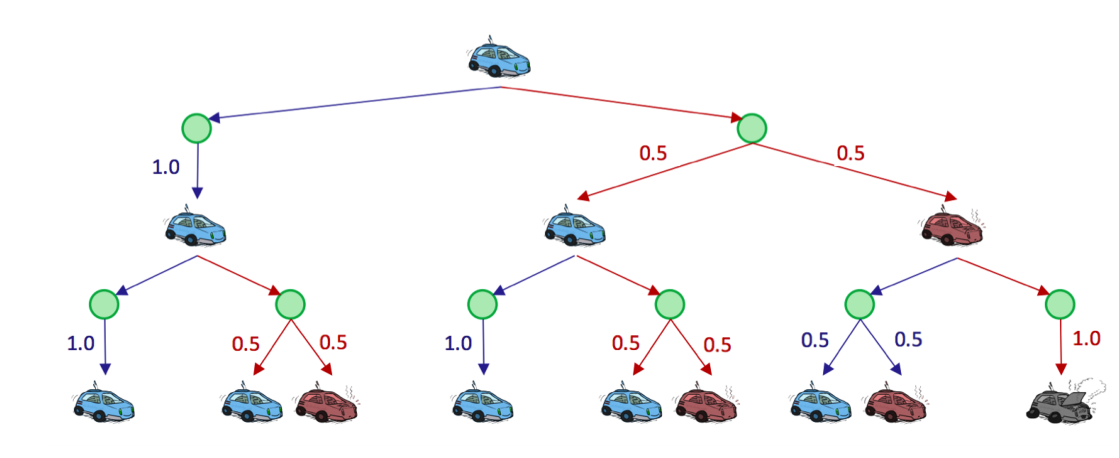
为了建模不确定性,在状态树中我们引入$q-state$节点(上图中的绿点)与正常的$state$节点区分,一条$state$节点到$q-state$节点的边代表一个action,$q-state$到$state$的边则代表采取该行动后转移到目标状态的概率。
显而易见,MDP符合Principle of Optimality. 它对应的贝尔曼方程如下:
$$
V^{}(s)=\underset{a}{max}\underset{s’}{\sum}\space T(s,a,s’)[R(s,a,s’)+\gamma V^{}(s’)]
$$
甚至可以更清晰的解释该方程,我们引入$Q(s,a)$表示从状态$s$采取行动$a$到达的$q=state$的最优收益。其计算式如下:
$$
Q^{}(s,a)=\sum_{s’}T(s,a,s’)[R(s,a,s’)+\gamma V^{}(s’)]
$$
进一步有:
$$
V^{}(s)=\underset{a}{max}\space Q^{}(s,a)
$$
事实上,如果能找到上述方程的一个解$V$,则必有$\forall s\in S.V(s)=V^{*}(s)$. 证明
Solve the Bellman Equation
Value Iteration
顾名思义,值迭代算法通过不断迭代$V$直到收敛来求解方程。
记第$i$次迭代时的Value Function为$V_{i}$, 同时它也代表在时间限制为$i$时的最大收益,算法具体流程如下:
$\forall s\in S.V_0(s)=0$
重复下面的更新,直到$\forall s,V_{k+1}(s)=V_k(s)$
$$
\forall s\in S,V_{k+1}(s)\leftarrow \underset{a}{max}\underset{s’}{\sum}\space T(s,a,s’)[R(s,a,s’)+\gamma V_k(s’)]
$$
时间限制为$k+1$时,从$s$转移到后继状态必然占用一个时间戳,因此其子问题变为时间限制为$k$。
这种迭代实质上是一种动态规划算法,以时间限制为计算顺序。
为什么收敛后一定与$V^{*}(s)$相等?
- 从时间限制的角度来看,每一次迭代都求得时间限制为$k$时的真实最优值,当这个$k=k_0$时收敛,说明$\forall k\ge k_0.V_k(s)=V_{k_0}(s)$. 也就是说时间限制再怎么放大甚至到无穷,最优值都是$V_{k_0}(s)$
Policy Extraction
仅仅得出MDP的最优值函数是不够的,我们真正需要的是其对应的Policy. 这个也很简单,当值函数收敛时,每一个状态与其最大的$q-state$之间的action即为Policy在这一步的取值。
$$
∀s ∈ S, π∗(s) = \underset{a}{argmax}
\space Q^∗(s,a) = \underset{a}{argmax}\sum_{s’}
T(s,a,s′)[R(s,a,s′)+γV ∗(s′)]
$$
为了减少重复计算,在Value Iteration时额外储存所有q-state节点的q-value,这样上式就只需要一个argmax操作即可
Policy Iteration
在Value Iteration中,每次迭代需要遍历$|S|$个状态,每个状态至多有$|A|$个actions,每个action至多会涉及$|S|$个后继状态。因此总的时间复杂度是$O(|S|^2|A|)$. 这还只是一次迭代。
实际上,我们真正需要的是optimal policy而非精确的optimal value,而policy收敛要比value快得多。(一个值函数可能并非$V^*$,但其在收敛到$V^*$的过程中可能policy不会改变了)。Policy Iteration算法就是只让Policy收敛即可,算法流程如下:
定义一个初始的policy,可以是随机的,也可以用一些启发式方法使其接近optimal policy加快收敛
重复以下操作直到收敛,即$\forall s\in S.\pi_{i+1}(s)=\pi(s)$:
对当前的policy进行评估。定义$V^\pi(s)$为在采取policy $\pi$的情况下从$s$出发获得的实际收益。policy evaluation就是计算所有$s$的$V^\pi$, 即取遍$s\in S$,求解下列方程组成的系统。
$$
V^\pi(s)=\sum_{s’}T(s,\pi(s),s’)[R(s,\pi(s),s’)+\gamma V^\pi(s’)]
$$当对目前policy有评估后,就可以利用这个评估优化policy。
$$
\pi_{i+1}(s)=\underset{a}{argmax}\sum_{s’}T(s,a,s’)[R(s,a,s’)+\gamma V^{\pi_i}(s’)]
$$
算法正确性:第一次迭代会使得termial state上层节点采取正确的policy,后续迭代则会将这种正确性自底向上传递。因此,理论上迭代到最后一定会达到optimal policy,而收敛使得迭代结果不再改变,因此是为optimal policy。