零和博弈问题的求解策略 | CS188 Project 2 的实验分享

在传统的搜索问题中每一步的状态转移都是已知的(即一个状态可以转去哪些状态，代价分别是多少)，因此我们只需要搜到一条通往goal state的路径然后perform一下就好。但在博弈问题中，由于对手的存在我们并不能确定某个状态会转移到哪个其它状态。换句话说，在博弈问题中我们对状态转移没有完全控制权。因此，传统的搜索技术无法应用于这些问题。在本文中我们先来研究最简单的确定性零和博弈。确定性是指博弈过程中的行为都是确定的，不存在随机性；零和指我方的收益与对方的损失相当。

可以这样简单地想：在零和博弈中存在一个变量$X$，我方想要最大化$X$的取值而敌方则要最小化。双方的收益取决于同一个变量，这就是零和博弈最大的特征。

Minimax

我们首先做出如下假设：敌方的行为总是趋向于最小化$X$的值，即使得我们的状态最差；而我方总是趋向于最大化$X$的值。有了这样一个假设，双方在不同状态下如何迁移就都固定了，我们又重掌了对状态转移的完全控制权。

为了更精确地描述算法，我们形式化地定义博弈树如下：

terminal utilities: 博弈结束状态的收益值，在一场博弈中属于先验知识。
state value: 一个状态的取值表示从这个状态出发agent所能获得的最大收益。

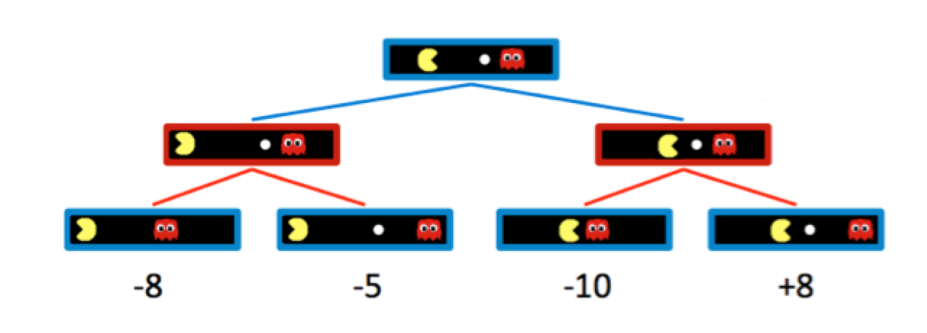
在上图所示的博弈树中，蓝色为我方控制的状态，红色为敌方控制的状态。根据我们之前做出的假设，terminal utilites将不断向上传播到根节点(具体实现为dfs)，传播的规则如下：

$\alpha-\beta$ Pruning

只要我们在最大最小值算法中的假设成立，该算法看似完美——即使敌人处处“为难”我们，我们也总能选取最终获得最大收益的行为。但该算法实际的时间复杂度为$O(b^m)$. ($b$指每个节点的最大分支数, $m$指树的高度). 我们必须采取一些手段缩减搜索空间，提高搜索效率。

Alpha-Beta剪枝的核心思想很简单：在遍历$n$的children时，一旦发现此时$n$的取值不可能被$n$的parent采用时，就停止对children的遍历。在有了剪枝后，算法复杂度缩减为$O(b^{\frac{m}{2}})$, 这使得我们原来可解的搜索深度扩大了一倍。

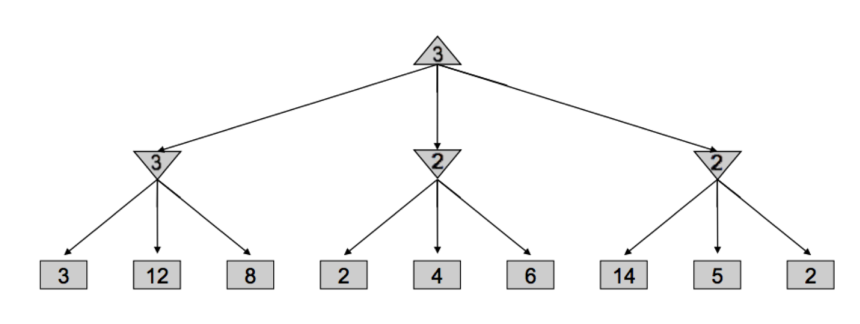
下面来看一个简单的例子，在遍历中间结点$n$(图中第二层为2的结点)的children时，首先访问到2，因为$n$是最小值结点，因此$val(n)\leq 2$. 而$n$的父结点取值却$\geq 3$. $n$不会被父结点考虑了，因此就不用再继续遍历$n$的孩子了。

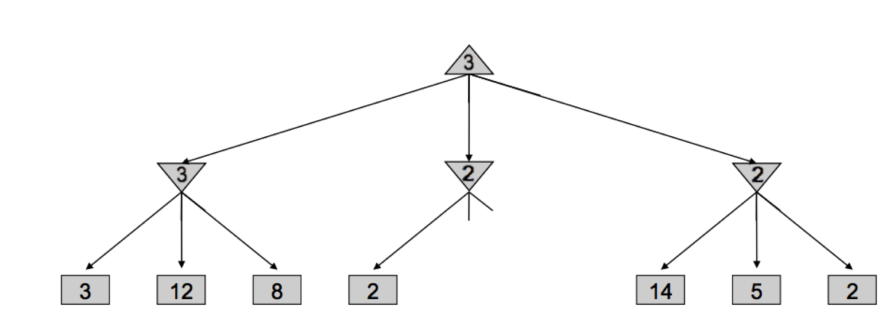
伪代码如下：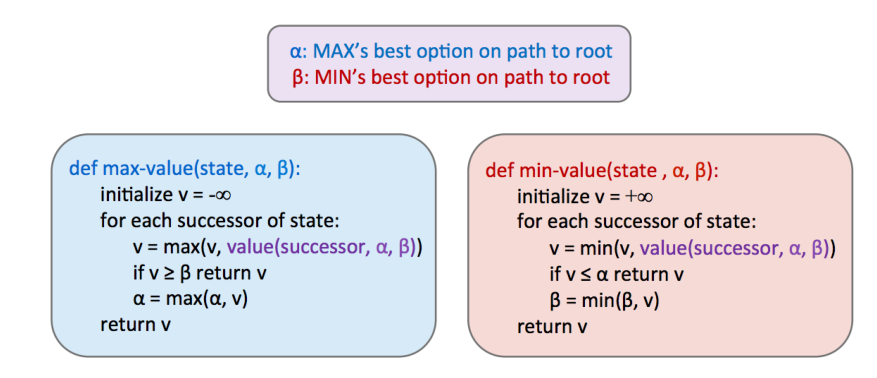

Evaluation Function

当状态空间非常大时，搜索深度不能太大。但最大最小值算法要求我们必须搜到叶节点才能将terminal utilities传播上去。为了解决这个问题，我们的想法是为非叶节点提供评估函数估计其state value然后向上传播。

这种办法使得状态空间很大的问题也能应用最大最小值算法求解，但由于评估函数并不是真实值，所以最后根节点的收益不一定是最佳的。

评估函数的真实性会显著影响该算法找到最佳收益的能力。一般来说，评估函数是状态特征的线性组合。即:

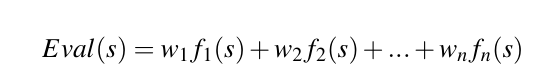
$f_i(s)$是从状态$s$中提取出一些可被量化的特征。比如五子棋中当前连四子的个数
$w_i$是每个特征的权重，用于区分不同特征的重要程度。比如一些特征有利于敌方，那么$w$应当是负的。

Expectimax

上述三种trick构成了解决确定性零和博弈问题的框架，它们依赖于一个重要的假设即对方的行为是确定的且总是试图最小化我方的收益。但当对方的行为并不总是确定的而是有一定概率(已知)时，就需要对敌方的行为做出修正。办法是取敌方控制的状态的数学期望值。

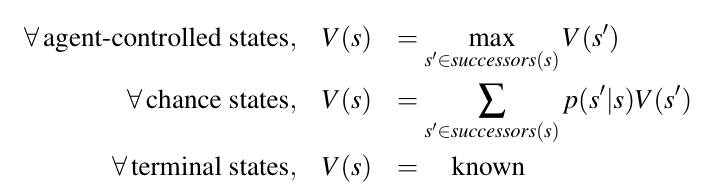
这个模型可以应对两种情况，一种是敌方的行为的结果是非确定的，每一步行为有概率$p$导致状态发生$s\to s’$的变化；另一种是敌方行为的结果确定但采取使得$s\to s’$的行为的概率为$p$

Utilities

上面讨论的4种算法已经能cover确定性零和博弈以及部分非确定性零和博弈了，它们能够在特定情况下找出使我方utilities最大的博弈策略。但我们还没有形式化地定义utility。事实上，utility是衔接计算本身与agent行为的关键，计算只是最大化utility，因此只有utility与rational高度相关时，我们的agent才能表现出ration. 所以合理地定义utility十分关键。

考虑如下定义：

在B和A + $1中，agent偏向B
在C和B + $1中，agent偏向C
在A和C + $1中，agent偏向A

现假设agent持有A，对手持有B和C，那么经过交换A将一无所有还搭上了$3…显然不够理性。可见，定义合理的utility是agent表现出理性的关键。下面我们来形式化地定义它：

定义agent总是需要在不同的price和lottery中做出抉择，price指一个固定的价值，lottery则根据固定的概率展现不同的price，以两个price为例：
$$
L=[p,A;(1-p),B]
$$

如果agent在price $A,B$ 中偏向于$A$，记为$A\succ B$
如果agent在price $A,B$ 中没有偏好，记为$A\sim B$

要想agent表现出理性，那么它对不同物体的偏好应当满足如下公理：

有序性：$(A ≻ B)∨(B ≻ A)∨(A ∼ B)$
传递性：$(A ≻ B)∧(B ≻ C) ⇒ (A ≻ C)$
连续性：$A ≻ B ≻ C ⇒ ∃p[p, A; (1− p), C] ∼ B$

当$B$在偏好序列的中间时，可以构造出一个有关$A,C$的lottery使得它和$B$的价值令agent没有偏好
替代性：$A ∼ B ⇒ [p, A; (1− p), C] ∼ [p, B; (1− p), C]$
单调性：$A ≻ B ⇒ (p ≥ q ⇔ [p, A; (1− p), B] ⪰ [q, A; (1−q), B]$

上述公理只刻画了不同price、lottery之间的偏好顺序，然而要想被计算，我们还需要定义效用函数$U$将这些偏好顺序变为数值上的顺序。很直观地，我们只需要保证$U$满足如下规则即可：

$U(A) ≥ U(B)⇔A ⪰ B$
$U([p_1, S_1; … ; p_n, S_n])= ∑_ip_iU(S_i)$

事实上，对于lottery，公理中并没有给出它和price或是其它lottery直接相比的规则，但赋予数值后它们都不可避免地可比了。而不同的效用函数会使这部分结果不尽相同，这也是符合理性的。因为人在概率事件上的表现也并不相同，有的人偏向保守，有的人偏向冒险。下面我们以一个例子说明：

假设有三个效用函数$U_1(x)=x,U_2(x)=\sqrt{x},U_3(x)=x^2$

现有如下两个物体可被选择：$o_1=500$, $o_2$是一张彩票，有50%的概率获得1000元。分别代入上述函数，$U_1$在两者之间没有偏好，$U_2$偏向保守，会选择$o_1$, 而$U_3$偏向冒险会选择$o_2$。这种结果从理性上也是说得通的

Project 2

Q1 Reflex Agent

Reflex Agent就是不考虑行为的结果，单纯基于当前状态做出反应。有点类似于”贪心”思想。这道题目要求实现一个Reflex Pacman避开所有ghosts并吃到所有food. 实现很简单，根据当前状态扩展出Pacman可能的后继状态，利用评估函数为每个后继状态评分并选择最优的那一个。评估函数也很好写:

先判断是否会遇到ghost，如果会则直接pass
再判断是否吃到了food，如果吃到则返回一个很大的收益
上述都不满足时，计算距离所有food的曼哈顿距离，返回最小距离的倒数

上述算法其实相当简化：

后继状态中ghost的位置有多种可能(四个方向)，为了简便我直接取它在上一个状态的位置+方向形成的新位置(事实上ghost可以变向)，因此依然有可能被吃掉
在有障碍物时，计算曼哈顿距离可能会导致pacman一直处于stop状态。如下图所示，当前Pacman所处位置其实是曼哈顿距离最短的，因此按照上述算法不走才是最优解。但计算真实距离又太慢了

好在这道题测试用例中并没有障碍物，做Q1也只是体验一下reflex agent，没必要深究。值得花时间当然是后面的plan agent啦

Q2 Minimax

很常规的写代码，没什么特殊的

def getAction(self, gameState):
    nextIsPacman = lambda agentIdx: agentIdx == gameState.getNumAgents() - 1

    def miniMax(currentState, agentIdx, depth):
        if currentState.isWin() or currentState.isLose() or depth == self.depth + 1:
            return (self.evaluationFunction(currentState), 'Stop')
        valueFunc = None
        nextAgentIdx = (agentIdx + 1) % currentState.getNumAgents()
        if nextIsPacman(agentIdx):
            depth += 1
            if agentIdx == 0:
                valueFunc = max
            else:
                valueFunc = min
                legalActions = currentState.getLegalActions(agentIdx)
                successorValues = [miniMax(currentState.generateSuccessor(agentIdx, action), nextAgentIdx, depth) for action in legalActions]
                retValue = valueFunc(successorValues)
                print(retValue)
                action = legalActions[successorValues.index(retValue)]
                return (retValue[0], action)
            
     return miniMax(gameState, 0, 1)[1]

值得注意的是，因为最终要返回最大value对应的action. 因此需要将action作为返回值一层层传递出去

Q3 Alpha—beta pruning

依然是很常规的写代码。稍微值得注意的是这道题目中max和min并不是交替的，而是有多个min层。但这并不影响alpha beta剪枝算法的核心，只需要根据agentIndex判断下一层是什么层即可

def getAction(self, gameState):
        nextIsPacman = lambda agentIdx: agentIdx == gameState.getNumAgents() - 1
        myMax = lambda x, y: x if x[0] > y[0] else y
        myMin = lambda x, y: x if x[0] < y[0] else y
        def maxValue(currentState, agentIdx, nextDepth, alpha, beta):
            maximal = (-9999, None)
            nextAgentIdx = (agentIdx + 1) % currentState.getNumAgents()
            legalActions = currentState.getLegalActions(agentIdx)
            for action in legalActions:
                successorState = currentState.generateSuccessor(agentIdx, action)
                maximal = myMax(maximal, (genericValue(successorState, nextAgentIdx, nextDepth, alpha, beta)[0], action))
                if maximal[0] > beta:
                    return maximal
                alpha = max(alpha, maximal[0])
            return maximal

        def minValue(currentState, agentIdx, nextDepth, alpha, beta):
            minimal = (9999, None)
            nextAgentIdx = (agentIdx + 1) % currentState.getNumAgents()
            legalActions = currentState.getLegalActions(agentIdx)
            for action in legalActions:
                successorState = currentState.generateSuccessor(agentIdx, action)
                minimal = myMin(minimal, (genericValue(successorState, nextAgentIdx, nextDepth, alpha, beta)[0], action))
                if minimal[0] < alpha:
                    return minimal
                beta = min(beta, minimal[0])
            return minimal

        def genericValue(currentState, agentIdx, depth, alpha, beta):
            if currentState.isWin() or currentState.isLose() or depth == self.depth + 1:
                return (self.evaluationFunction(currentState), 'Stop')
            if nextIsPacman(agentIdx):
                depth += 1
            if agentIdx == 0:
                return maxValue(currentState, agentIdx, depth, alpha, beta)
            else:
                return minValue(currentState, agentIdx, depth, alpha, beta)
        return genericValue(gameState, 0, 1, -9999, 9999)[1]

Q4 Expectimax

def getAction(self, gameState):
        nextIsPacman = lambda agentIdx: agentIdx == gameState.getNumAgents() - 1
        myMax = lambda x, y: x if x[0] > y[0] else y
        def maxValue(currentState, agentIdx, nextDepth):
            maximal = (-9999, None)
            nextAgentIdx = (agentIdx + 1) % currentState.getNumAgents()
            legalActions = currentState.getLegalActions(agentIdx)
            for action in legalActions:
                successorState = currentState.generateSuccessor(agentIdx, action)
                maximal = myMax(maximal, (genericValue(successorState, nextAgentIdx, nextDepth)[0], action))
            return maximal
        
        def chanceValue(currentState, agentIdx, nextDepth):
            expection = 0
            nextAgentIdx = (agentIdx + 1) % currentState.getNumAgents()
            legalActions = currentState.getLegalActions(agentIdx)
            for action in legalActions:
                successorState = currentState.generateSuccessor(agentIdx, action)
                expection += genericValue(successorState, nextAgentIdx, nextDepth)[0]
            return (expection / len(legalActions), None)

        def genericValue(currentState, agentIdx, depth):
            if currentState.isWin() or currentState.isLose() or depth == self.depth + 1:
                return (self.evaluationFunction(currentState), 'Stop')
            if nextIsPacman(agentIdx):
                depth += 1
            if agentIdx == 0:
                return maxValue(currentState, agentIdx, depth)
            else:
                return chanceValue(currentState, agentIdx, depth)
        value = genericValue(gameState, 0, 1)
        return value[1]

Q5 Better Evaluation Function

根据笔记中对评估函数的描述，我们只需要将一些重要的特征提取出来然后赋予合适的权重即可。

这道题目中我取出的特征是距离ghost的距离和距离食物距离的倒数，然后通过“调参”确定了还可以的权重。

整个过程中有点奇怪的地方是，在food只剩1-2个的时候，pacman会一直原地上下晃动而不是去吃food。原因在于我的参数使得吃那1-2个food的收益小于远离ghost的收益，所以我就特判了一下在food数量较少时提高food的权重。

这部分代码因人而异就不放出来了。

总结

这次的project比较简单，需要自己思考的内容不多，主要还是实现几个博弈树算法。但让我觉得有点惊喜的是，在Q5中切实体会了一把“调参”的感觉，即使是这样一个简单的问题，依然可以不仔细思考参数的作用而凭直觉调整来看效果。

图10

CS188-P3 Game