Constraint Satisfaction Problem(CSP)的求解

Constraint Satisfaction Problem

Definition

直观来讲, 约束满足问题(CSP)就是要求一组变量在给定的约束条件和值域下是否有解。

形式化地定义CSP为$<X,D,C>$，其中:

$X={X_1\dots X_n}$是一组可被赋值的变量
$D={D_1,\dots D_n}$是相应变量的值域，记其中最大大小为$d$
$C={C_1,\dots,C_n}$是一组约束。约束可能涉及任意多变量，比如限制某个变量的取值，要求某两个变量的取值要满足一定约束，甚至是很多个变量之间的约束。

CSP问题的一个解是指存在一种赋值既complete(所有变量均被赋值)又consistent(所有约束均满足)。对于CSP问题我们通常有如下需求^1：

找出一种解即可
找出所有解
找到一个最优解(optimal is problem specific)

上述形式化定义的CSP是NP-hard问题，即时间复杂度为$O(d^n)$，但不代表每一个具体的CSP都无法高效求解。举一个极端的例子，当$C$是空集时，该问题实例可在$O(1)$时间求解(任意complete赋值均满足)。

一般的CSP怎么求解呢？至今还没有一个多项式复杂度的算法。但有一些trick或启发式方法能够尽可能提高效率，此外如果某个CSP满足一定的结构，我们甚至可以在很低的时间复杂度内求解。下面来看一些常用的手段：

Backtracking

先不考虑各种trick, 最trivial的办法就是遍历所有可能的赋值，然后验证每一种赋值是否consistent. 这可以通过dfs轻松做到。然而，当某个赋值已经使得某一条约束条件不满足时就没有必要继续遍历这一组赋值了，而是向前回溯修改之前的赋值。因此，回溯提高求解效率的关键就是当某个赋值已经显然地使得限制不成立时不再继续这条路径的遍历。

上述dfs仅指遍历的顺序，不保存已经遍历过的状态，因此需要到一次遍历到底时才可以判断是否一致。事实上，在dfs的实现中保存当前遍历路径的状态后,它和回溯算法实现就没有什么两样了。

Filtering

上面说到回溯法是在某些限制条件显式地不满足时略去剩下的遍历，这是最直接的削减搜索空间的办法。有时候，对一个变量的赋值虽然没有显式地触发限制，但它会使得其它变量可取的值减少，即间接地影响需要访问的状态。很显然，对于一个赋值操作，我们对它的间接影响发现的越多，搜索空间就越小，但也会随之带来越大的额外计算量，这是需要平衡的。在此，我们介绍两种较为简单的发现间接影响的办法：

forward-checking

核心思想是在给变量$X_i$赋值$V_1$后，削减与$X_i$相邻变量值域中跟$V_1$冲突的值。这种办法实现起来很简单，但对$X_i$的赋值只将其影响传播到与其相邻的变量。实际上这种影响将会在全图传播，下面我们来看实现这种思想的办法：

arc consistency

CSP图一般是无向图，因为边代表二元限制，具有可交换性。但由于我们的赋值是有固定顺序的，为了表示影响的传播方向，需要构造一个有向图。很显然，将一个无向图改造成有向图只需要把每一条边改变为方向相反的两条有向边即可。这样的一条有向边称为arc. 具体的算法流程如下：

将所有的arcs存入一个队列$Q$
迭代地从$Q$中取出一个arc，记为$X_i\to X_j$. 对于$X_i$当前可取的每一个值$v$，都验证是否存在$X_j$的取值$w$使得$<X_i=v,X_j=w>$不违反任何约束。如果$w$不存在则从$X_i$取值集合中移除$v$
如果在上述过程中$X_i$确实有值被移除，则将所有未赋值变量对应的arc$X_j\to X_i$加入$Q$(如果已经存在则无需重复加入)
重复上述迭代，直到$Q$为空(意味着已赋值的变量具有arc consistency)，或某个未赋值变量取值集合为空(意味着继续赋值必然会违反约束，需要回溯)

上述算法如果未触发回溯，说明当前的赋值任意arc都满足arc consistency，其含义是对于任意两个变量$X_1,X_2$，当其中任意一个变量取一个consistent value时，另一个变量至少有一个consistent value可取。arc consistency只保证了当前已赋值的变量产生的影响传播到了全部变量，但并没有考虑未赋值变量组合起来产生的影响，如下图中第一例。$k-consistency$定义为对于任意$k$个变量，取其大小为$k-1$的任意子集赋consistent value, 则第$k$个变量至少有一个consistent value可取。arc consistency就是$k=2$时的特例，事实上$k$越大，满足其一致性时有解的可能性就越高，但求解速度就越慢。

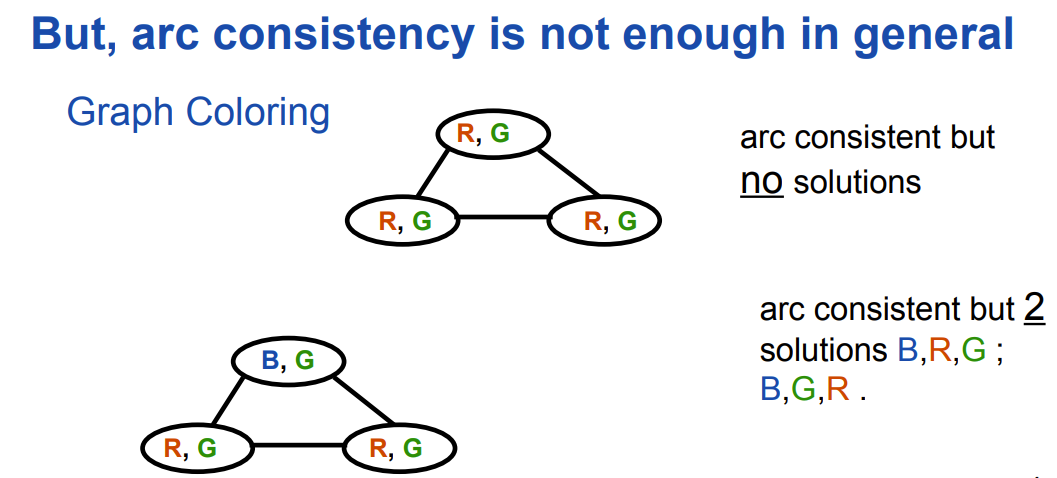
但仍然值得注意的是，如果某个满足arc consistency的状态未赋值变量的值域都只剩一种可能取值，此时则可确定该CSP有解。

Ordering

利用回溯搜索技术求解CSP时显然要遵循一定的迭代顺序，上面的算法中我们都忽略了这一点，采用一个随机顺序而已。但实际上，顺序也能影响效率。这背后其实是一个启发式想法：提高可能是可行解状态的优先级。

在选择哪一个变量接下来被赋值时，应该选择当前值域最小的变量。因为可行解要求每个变量都被赋值(complete)，而值域最小的变量受其它变量赋值的影响可能最大，因此应当先满足它再满足其它变量。

在选择具体将哪个值赋值给变量时，应当选择对其它变量值域影响最小的值。因为削减越多，其它变量越不容易成功赋值，这很直观。

Structure

当CSP图具有某种结构时，我们可以利用这种结构极大地缩小时间复杂度。比如当CSP图是一棵Tree时，时间复杂度将从$O(d^n)$降低到$O(nd^2)$:

在CSP图中任意选择一点作为root(树的性质: 任意节点都可作为root)
将所有无向边变为背离root的有向边
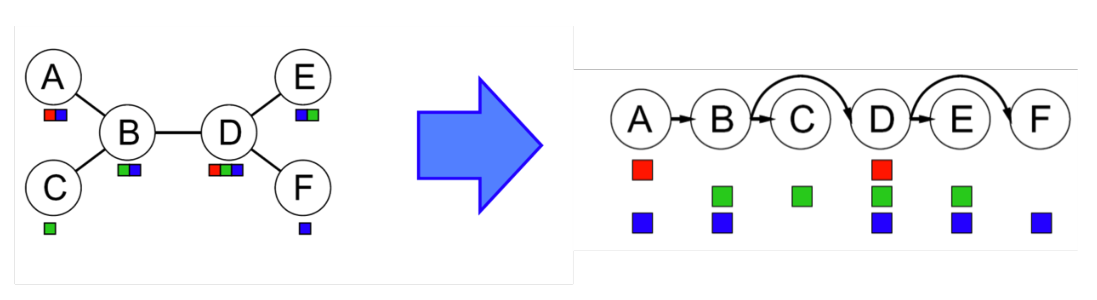
以下图为例，从最右侧的结点开始确保所有$Parent(X_i)\to X_i$这种arc的一致性(因为树的”单向性”，每个arc只需迭代一次)
如果所有arc的一致性成立，那从root开始依次赋值即可得出可行解。因为当我们严格按照parent->child的这种方式赋值时，每个变量的值域只会受其parent的影响，而通过上述对树的线性拓扑化，每个节点的parent唯一，换句话说每个节点的值域只会受其它一个节点的影响，而arc consistency保证在这种情况下存在解。

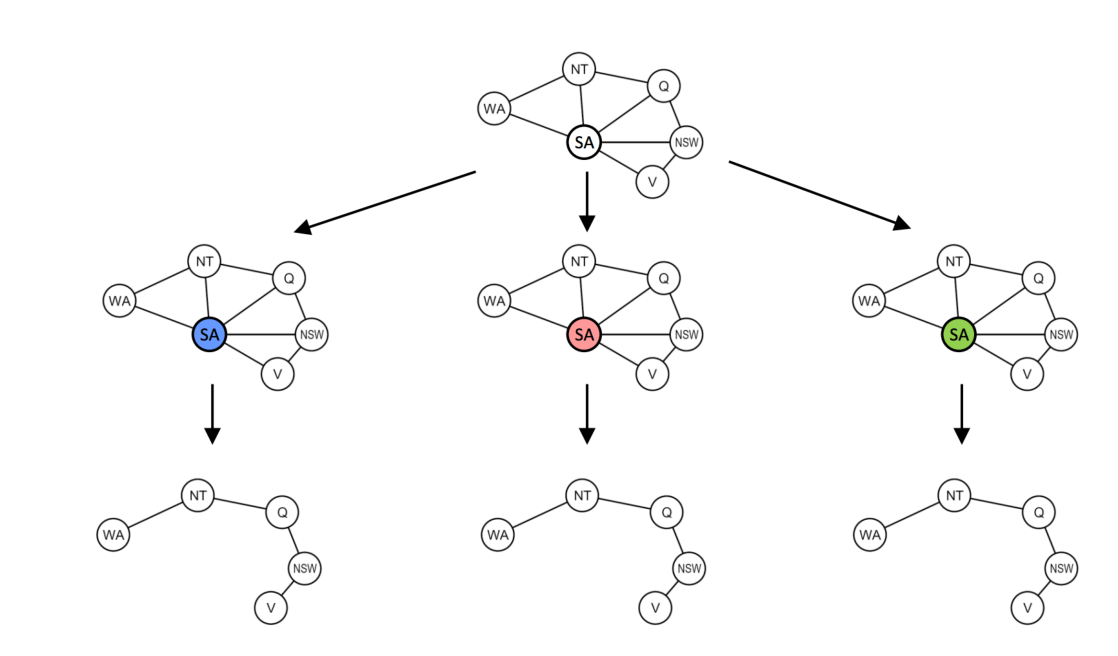
对于一些不是树的结构，定义cut set为去掉这些点后整个图就变成树。我们先求出最小cut set，然后先遍历minimal cut set的可能取值，削减树中变量的值域，然后对树中变量应用上述算法。

Local Search

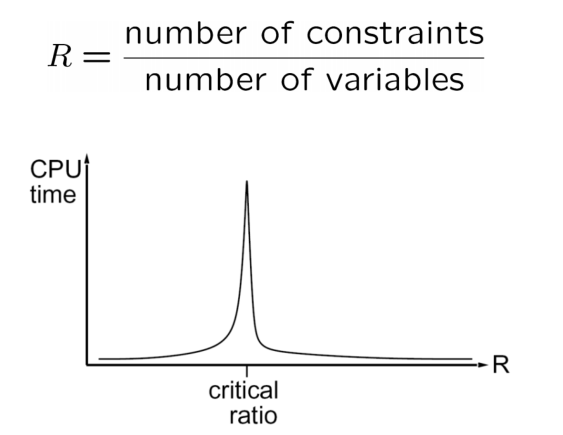
先对每个变量随机地赋值，然后不断地取破坏最多约束的变量，为它重新赋上破坏最少约束的值。

这种启发式方法在大多数情况下十分高效，甚至可以达到常数级，只有在少部分情况下会很慢，见下图。

CS188-P2 CSP